SpaceDrive：Infusing Spatial Awareness into VLM-based Autonomous Driving

Paper Title: SpaceDrive: Infusing Spatial Awareness into VLM-based Autonomous Driving

Paper Link: https://arxiv.org/abs/2512.10719

Project Page: https://zhenghao2519.github.io/SpaceDrive_Page/

Authors: Peizheng Li, Zhenghao Zhang, David Holtz, Hang Yu, Yutong Yang, Yuzhi Lai, Rui Song, Andreas Geiger, Andreas Zell

Affiliations: Mercedes-Benz AG, University of Tübingen, Tübingen AI Center, TU Munich, Karlsruhe Institute of Technology, University of Stuttgart, UCLA

Abstract

Vision-Language-Action Models (VLAs) are emerging as a new paradigm for end-to-end autonomous driving, leveraging their strong generalization and semantic understanding capabilities. However, existing 2D VLM-based driving systems exhibit significant shortcomings in handling fine-grained 3D spatial relationships, which are core requirements for spatial reasoning and trajectory planning. To address this, Mercedes-Benz and the University of Tübingen jointly propose SpaceDrive, a spatially-aware VLM-based autonomous driving framework. Its core innovation lies in abandoning the conventional VLM approach of treating coordinate values as text tokens, and instead introducing 3D Positional Encoding (PE) as a universal spatial representation. Specifically, SpaceDrive first explicitly fuses visual tokens with 3D PE in the feature space. It then uses the same universal 3D PE to replace the corresponding coordinate text tokens in the prompt, serving as the interface for the foundation model’s input and output. Furthermore, SpaceDrive employs a regression decoder instead of a classification head to predict planned trajectory coordinates, circumventing the inherent limitations of language models in numerical processing. Experiments show that compared to existing VLM/VLA methods, SpaceDrive achieves state-of-the-art (SOTA) performance in open-loop evaluation on nuScenes and ranks second in the closed-loop Bench2Drive evaluation with a driving score of 78.02, significantly improving planning geometric accuracy and safety.

Core Insights

Current VLM applications in autonomous driving face two fundamental limitations that constrain their potential as general driving agents:

• Disconnect between 2D Semantics and 3D Geometry: VLMs are primarily pre-trained on large-scale 2D image-text pairs, leading to a severe lack of 3D spatial priors. This results in ambiguous scene descriptions and defective spatial reasoning capabilities.
• Defects of Numerical Tokenization: In language models, coordinates are typically decomposed digit-by-digit into characters or numbers (e.g., “3.82” becomes “3”, “.”, “8”, “2”). This process essentially fits the joint distribution of tokens rather than performing numerical computation. It ignores the continuous, neighboring structure of numerical values (e.g., “3.72” is closer to “3.82” than “3.12”) and averages the importance of tokens from different digit positions (e.g., equal loss weight for “3” and “2” in “3.82”), fundamentally limiting the accuracy and stability of continuous numerical prediction.

Existing VLM-based planners often overlook these issues or resort to training specific embeddings/queries for particular tasks to predict coordinates, making them difficult to transfer to upstream reasoning or other tasks.

However, the Positional Encoding (PE) within the Transformer architecture inherently handles positional relationships between tokens, which can be viewed as spatial relationships between semantic features. Inspired by this, SpaceDrive replaces textual numerical tokens with an explicit, unified 3D Positional Encoding. This converts coordinate descriptions into a unified representation that is computable, alignable, and directly usable by attention mechanisms, thereby enhancing the system’s spatial reasoning and trajectory planning capabilities.

Method

The core of the SpaceDrive framework is its unified spatial interface:

• Visual Side: A frozen depth estimator obtains absolute depth for each image patch, which is projected to 3D coordinates. These coordinates are then encoded by a PE module and added to the corresponding visual tokens, yielding spatial-aware visual tokens.
• Text Side: After tokenization, the text is scanned for coordinate expressions. Their numerical values are parsed and encoded by the same PE encoder to produce spatial tokens, which replace the original sequence of number tokens. A special prefix indicator ⟨IND⟩ marks these tokens.
• Output Side: The language head generates text normally. When ⟨IND⟩ is generated, the subsequent hidden state is fed into a PE decoder to directly regress 3D/BEV coordinates, replacing the digit-by-digit generation of numbers.

Perception Phase: Explicit Fusion of Vision and Depth

While using a VLM’s pre-trained visual encoder to extract visual tokens, SpaceDrive employs a frozen depth estimator (e.g., UniDepthV2) to obtain absolute depth. Combining this with camera intrinsics and extrinsics, the center of each image patch is projected into metric 3D space \(\mathbf{c}_p = (x_p^{3D}, y_p^{3D}, z_p^{3D})\). These 3D coordinates are mapped to a PE vector \(\phi(\mathbf{c}_p)\) of the same dimension as the tokens by a universal PE encoder. To avoid confusion with the base VLM’s RoPE, SpaceDrive adopts Sine-cosine encoding as the PE encoder:

\[\phi(\mathbf{c}_p)=\big[\phi_x(x_p^{3D}),\phi_y(y_p^{3D}),\phi_z(z_p^{3D})\big]\in\mathbb{R}^{dim}, \text{with} \\\] \[\phi_a(p_a) =\begin{cases} \sin(\tfrac{p_a}{20000^{2i/d_a}}),\\ \cos(\tfrac{p_a}{20000^{2i/d_a}}), \end{cases} i=0,\dots,\lfloor\tfrac{d_a}{2}\rfloor-1,\\\] \[d_x=d_y=\lceil\tfrac{dim}{3}\rceil, d_z={dim}-d_x-d_y.\]

The channels of the above 3D PE are allocated along the \(x/y/z\) dimensions. This 3D PE is then directly added to the modality-aligned visual token \(h_p\), thereby infusing the VLM’s visual input with absolute spatial coordinate information:

\[\tilde{h}_p = h_p + \alpha_{PE}\, \phi(\mathbf{c}_p).\]

Considering that sparse queries (like in Q-Former) are difficult to densely align with specific 3D locations and require additional alignment pre-training, visual tokens in SpaceDrive are aligned with the language space via an MLP projector. The \(\alpha_{PE}\) in the formula is a learnable normalization factor to avoid training instability caused by deviation of the token norm distribution from the pre-training distribution.

Spatial Information Retrieval: Since attention is based on dot-product similarity retrieval, adding 3D PE to visual tokens essentially makes spatial location a key-value structure directly retrievable by attention. Consequently, coordinate PEs in subsequent text can use similarity to index semantic features at corresponding spatial locations, rather than relying on the language model to guess.

Reasoning Phase: Unified Coordinate Interface

When 3D coordinates appear in the input prompt, for a coordinate substring \(S_r\) in the text prompt, its numerical value \(\mathbf{c}_r = (x_r,y_r,z_r)\) is extracted and encoded using the same unified PE encoder \(\phi(\cdot)\). These encoded 3D PEs replace the original sequence of number tokens and are preceded by the special token ⟨IND⟩ to avoid semantic confusion (for special cases like BEV coordinates, e.g., trajectory waypoints, the \(z\)-axis component in the PE is set to 0 to avoid affecting attention calculation).

\[\tilde{h}_i=\begin{cases}\phi(\mathbf{c}_r) & i\in\mathcal{S}_r \\ \mathrm{Tokenizer}(t_i) & \text{otherwise}\end{cases} .\]

In addition to basic prompt input, the vehicle’s Ego Status has proven highly effective for trajectory planning. Existing methods typically encode all state variables (e.g., pose, velocity, acceleration) into a single vector embedding \(\mathbf{e}_{\text{ego}}\in\mathbb{R}^{dim}\). Benefiting from the unified spatial representation, SpaceDrive can also encode historical Ego waypoints using the same \(\phi(\cdot)\) and input them along with \(\mathbf{e}_{\text{ego}}\) as explicit spatiotemporal conditions to the language model for precise trajectory planning.

Logical Consistency: By using the same set of PE for vision, text prompts, and Ego waypoints, the model is compelled to learn a unified spatial semantic indexing, rather than learning disjointed mappings for different modalities.

Output Phase: Regression Over Classification

During output generation, when the model’s language head predicts the special indicator token ⟨IND⟩ from \(\mathbf{e}_j\), the next step’s embedding output \(\mathbf{e}_{j+1}\) will be decoded into 3D coordinates by a dedicated PE decoder \(\psi(\cdot)\):

\[\hat{\mathbf{c}} = \psi(\mathbf{e}_{j+1}), \, \hat{\mathbf{c}} \in \mathbb{R}^3.\]

Considering that Sine-cosine PE is not analytically invertible (phase/frequency aliasing), the PE decoder is made learnable. This decoder can employ an MLP for deterministic coordinate regression output or choose a generative module like a VAE for multi-modal output. SpaceDrive defaults to using a lightweight MLP as the PE decoder.

Loss Function

For coordinate prediction, SpaceDrive employs Huber Loss for supervision, which balances outliers and convergence accuracy better than L2 or L1 loss. The text part retains the original cross-entropy loss:

\[\mathcal{L} = \mathcal{L}_{\text{LM}} + \mathcal{L}_{\text{Huber}}(\hat{\mathbf{c}}, \mathbf{c}).\]

Experiments and Visualization

The paper validates SpaceDrive and SpaceDrive+ (with Ego Status input) for open-loop and closed-loop planning on the nuScenes dataset and the Bench2Drive benchmark, respectively. In experiments, the framework is based on the Qwen2.5-VL-7B VLM, fine-tuned using LoRA alignment with a rank of 16. A frozen pre-trained Unidepthv2-ViT-L serves as the depth estimation module. For open-loop planning, the model predicts 6 points over a 3-second future horizon. Closed-loop planning follows SimLingo, outputting both path and speed waypoints for vehicle PID control.

Open-loop Planning (nuScenes)

To directly verify trajectory planning accuracy, an open-loop evaluation was first conducted. On the nuScenes dataset, SpaceDrive+ outperforms existing VLM-based methods like OmniDrive/ORION across all metrics (Avg. L2 = 0.32m, Avg. Collision = 0.23%, Avg. Intersection = 1.27%).

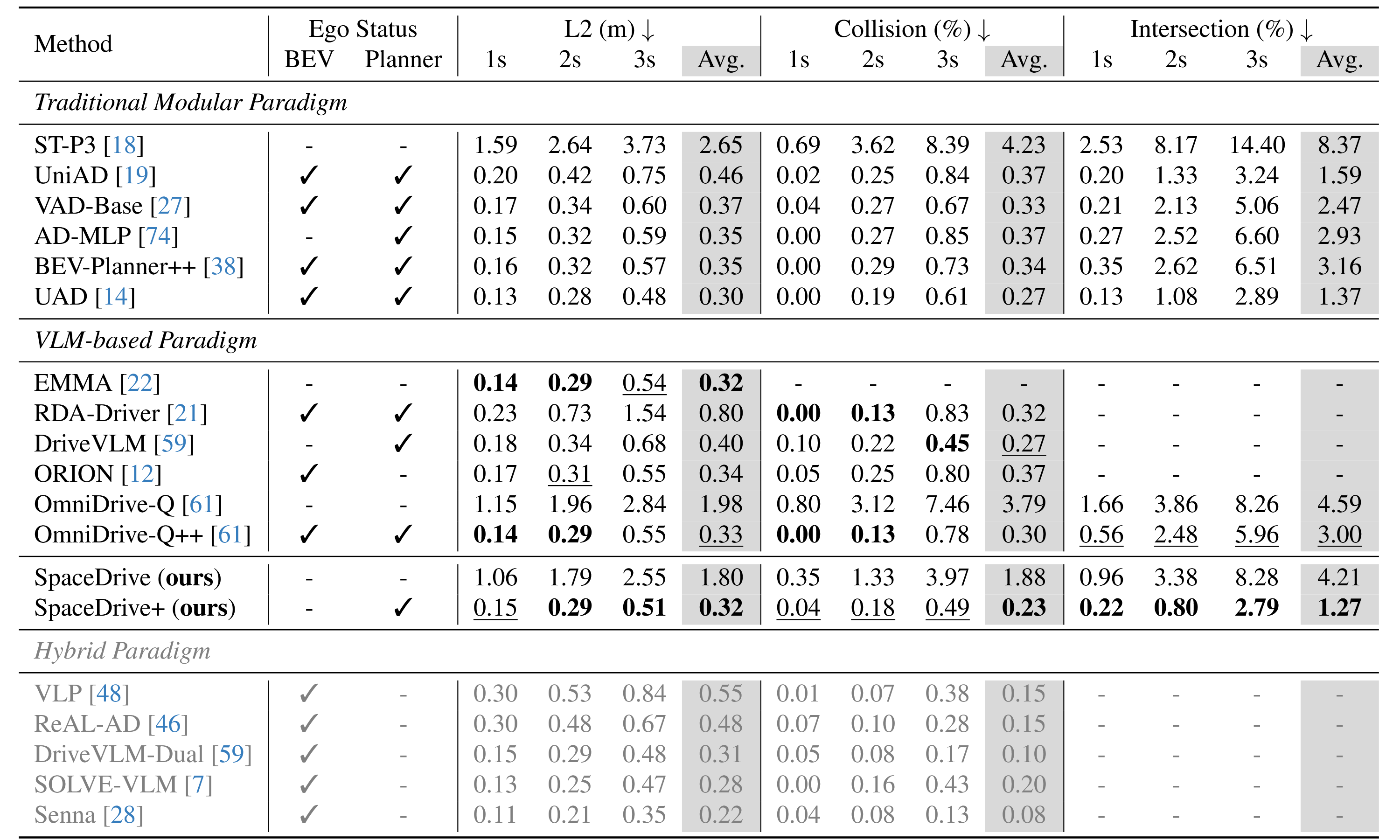
Notably: The SpaceDrive framework does not rely on BEV features at all. The results still demonstrate that the unified positional encoding interface is sufficient to support 3D spatial modeling within the VLM, architecturally reducing dependency on dense BEV representations.

Closed-loop Planning (Bench2Drive)

Considering that similarity-based open-loop planning evaluation is highly susceptible to dataset overfitting and cannot fully reflect a model’s actual driving capability, the paper further validates the method’s effectiveness in the closed-loop Bench2Drive benchmark.

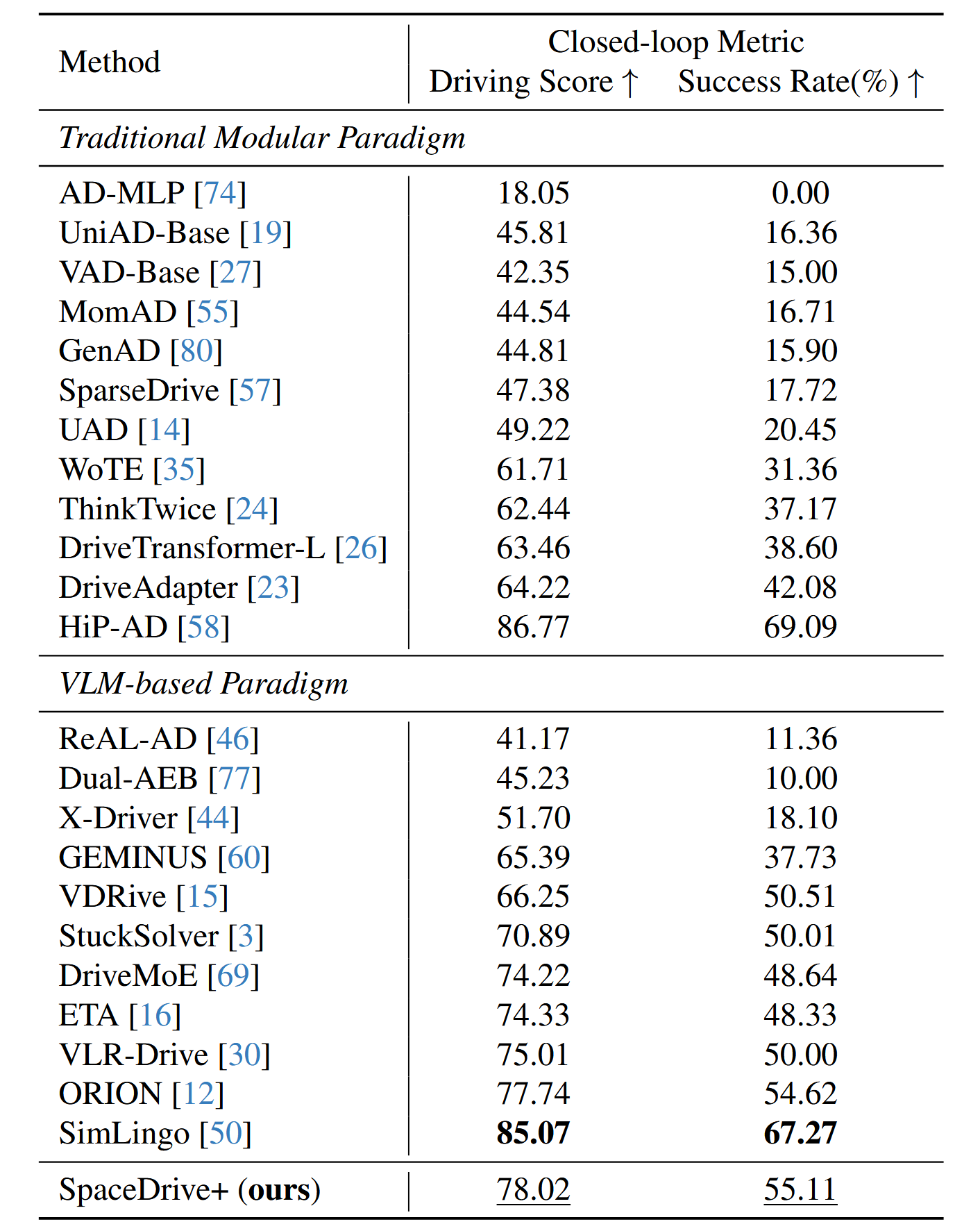
The paper first attempted a method using only text generation for trajectories. Experiments proved this method tends to degenerate into near-linear trajectories with oscillating headings in closed-loop, being highly unstable. This is because text generation essentially fits data priors rather than learning a controllable policy. In contrast, after introducing explicit universal spatial tokens, SpaceDrive+ achieves a Driving Score of 78.02 and a Success Rate of 55.11%, ranking second among VLM-based methods.

Visualization

The paper compares the performance of the pure text method and the method incorporating spatial tokens in the same scenario (lane change to avoid a cyclist):

• The pure text method’s output trajectory degenerates into a straight line with constantly oscillating direction, eventually causing the vehicle to swerve left significantly until colliding with a guardrail.

• SpaceDrive+ with spatial tokens, upon observing a slow cyclist ahead, first tentatively accelerates to seek an overtaking opportunity. Finding the adjacent vehicle does not yield, it decelerates to create a safe insertion gap, then decisively changes lanes, and corrects the steering in time before completing the lane change to avoid leaving the road.

Ablation Studies

To further validate how the universal 3D PE contributes to planning, numerous ablation studies were conducted, leading to the following conclusions:

• PE Injection Location is Crucial: Using PE only for text coordinate replacement without injecting it into visual tokens offers limited improvement (as PE cannot index corresponding visual features). Injecting 3D PE into visual tokens brings significant gains. When unified positional encoding is applied to both visual and text coordinate streams, planning performance improves regardless of ego state usage, highlighting the value of a shared spatial representation.

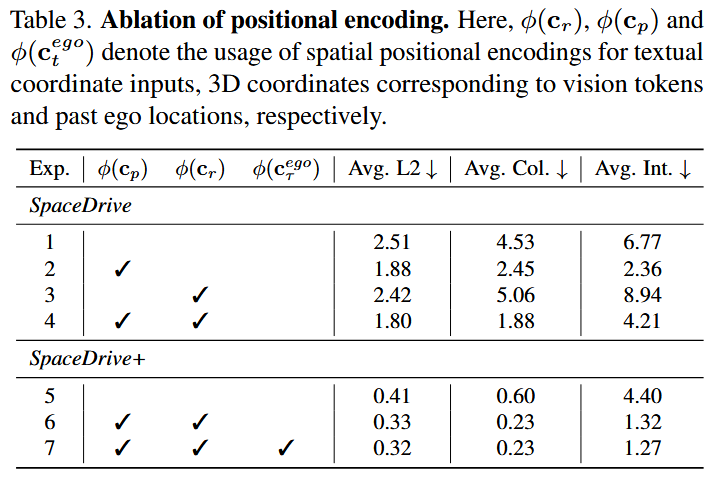
• Choice of PE Encoder/Decoder is Important: Sine-cosine encoding inherently offers better translation equivariance, aiding the attention mechanism in understanding spatial relationships between tokens, outperforming a learnable MLP encoder. RoPE conflicts with the base VLM’s RoPE, causing semantic instability in outputs. Directly inverting sine-cosine at the output is ill-posed, and the VLM’s output space is not fully aligned with its input embedding space. Therefore, a learnable, per-waypoint MLP decoder is superior.

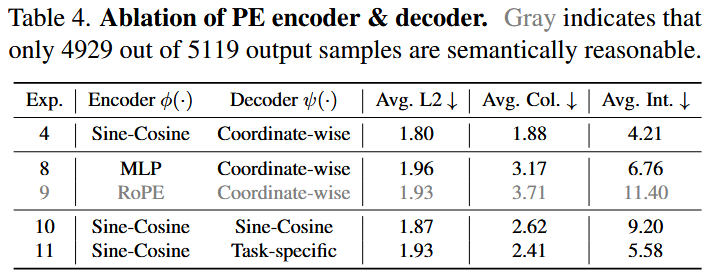
• Learnable \(α_{PE}\) is Important: Fixed-scale PE easily causes semantic instability or convergence difficulties, while a learnable α_{PE} significantly improves L2 error, collision rate, and out-of-bounds rate.

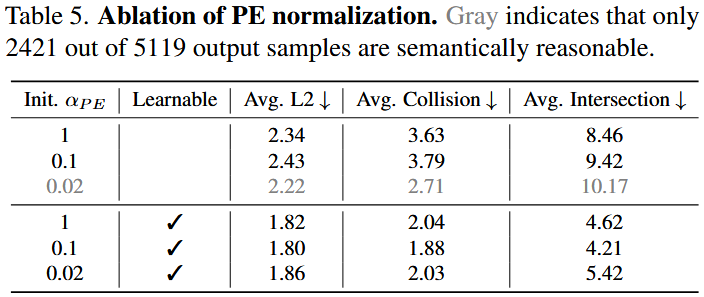
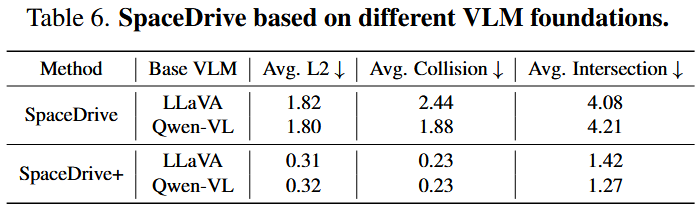
• PE Representation as an Interface is Transferable: The same set of PE spatial interface yields similar performance gains on both Qwen-VL and LLaVA, indicating that the benefits stem primarily from the unified spatial reasoning interface rather than specific adaptation to a particular base model.

Additionally, supplementary materials present more experiments related to VQA tasks, different depth estimation models, and various hyperparameters, further confirming the effectiveness of the proposed method.

Conclusion

SpaceDrive makes several key contributions to current autonomous driving and VLM research:

• Universal Spatial Representation: It introduces a unified 3D Positional Encoding that works consistently across perception, reasoning, and planning modules, representing a significant architectural innovation. This approach moves beyond task-specific embeddings towards more general spatial intelligence.
• Explicit 3D Understanding: Additively integrating spatial encoding with visual tokens creates an explicit link between semantic content and 3D location, enabling more accurate scene understanding and reasoning.
• Regression Respects Numerical Nature: By replacing digit-by-digit coordinate generation with regression-based dedicated decoding, SpaceDrive addresses a fundamental limitation of language models in handling continuous numerical quantities.
• Framework Generality: The method demonstrates compatibility with different VLM architectures (Qwen-VL, LLaVA) and proves suitable for inference-time enhancements like chain-of-thought reasoning, indicating broad applicability.

In summary, SpaceDrive provides a rigorous paradigm shift: from “modeling geometry with language” to “explicitly encoding geometry.” Its core contribution lies in demonstrating that within VLMs, a unified, modality/task-agnostic 3D positional encoding can effectively connect the perceived visual space with the planned physical space. This approach not only addresses the hallucination and accuracy issues of VLMs in large-scale spatial reasoning tasks but also preserves their general advantage in long-tail scene understanding. SpaceDrive represents a significant step towards enabling VLMs to interact effectively with the physical world through precise spatial understanding, pointing the way forward for more reliable and capable AI agents.